|
|
Materiales de estudio Navegación |
|
|
|
Posicionamiento por arco capaz de dos ángulos horizontales Autor: Roberto Garro |
||||
|
Utilizando las propiedades del arco capaz de cada uno de dos ángulos horizontales tomados a tres puntos visibles nos permitirá definir la posición del barco en el momento de tomar los dos ángulos. Será necesario que los tres puntos visibles están identificados en la carta de navegación. Los ángulos horizontales podrán ser tomados con un sextante o restando entre sí las marcaciones tomadas a los puntos de referencia. Recordatorio de definiciones geométricas aplicables a la construcción del Arco Capaz (ver) |
||||
|
Navegando en cercanías del Puerto de Mar del Plata seleccionamos tres puntos visibles y los identificamos en la carta:
|
||||
|
Datos obtenidos con la toma de ángulos horizontales:
|
||||
|
Construcción del arco capaz del segmento AB |
||||
|
El primer ángulo horizontal
tomado fue entre los puntos A y B Unimos en la carta ambos puntos y obtenemos el segmento AB |
|
|||
|
Con vértice en
A dibujamos un
ángulo igual al tomado entre los puntos A y B Lo dibujaremos hacia el lado opuesto del que se encuentra el barco, veremos luego que esta semirrecta será una tangente en A a la circunferencia que será origen del arco-capaz |
|
|||
| Dibujamos la mediatriz del segmento AB |
|
|||
| Con origen en A dibujamos una semirrecta perpendicular al cateto a del ángulo |
|
|||
|
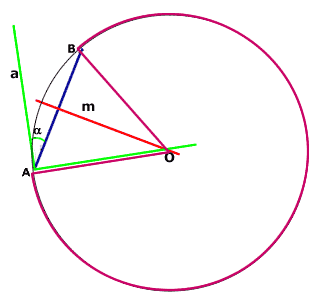
Esta semirrecta al cortar la mediatriz generará un segmento AO donde O es el centro de una circunferencia que conteniendo al punto A también contendrá al punto B. Entre los puntos A y B de la circunferencia se forman dos arcos AB, dentro de uno de los arcos se encuentra el centro O: este es el arco capaz AB. En un punto de este arco capaz estábamos al tomar
la medición del ángulo |
 |
|||
|
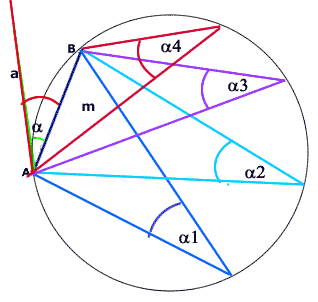
El ángulo a está semi-inscripto en la circunferencia y contiene al segmento AB. Todos los ángulos inscriptos en la circunferencia que contengan el segmento AB (a1, a2, a3 a4, etc. etc.) serán iguales entre si y a su vez iguales al ángulo semi-inscripto a |
 |
|||
|
||||